Skip to main content

底盘运动学 舵轮轮系

提示
  • 本文的运动学仅讨论机器人自身坐标系下的情况
  • 如需世界坐标系还需加上旋转矩阵

四舵轮轮系​

介绍演示​

轮系结构​

如图所示，建立如下世界坐标系 XOYXOY ，世界坐标系中 XX 正方向为机器人全局0度方向，建立机器人本地坐标系 xoyxoy ，车头方向为本地坐标系 xx 正方向。

机器人中心到每个轮子的xx、yy方向上的距离都为LL，机器人旋转角速度为ω\omega，逆时针方向为角速度正方向，机器人本体与轮子作为一个刚体，刚体中每个点的旋转角速度相等，因此有:

ω=ωLF=ωRF=ωLB=ωRB\omega = \omega_{LF} = \omega_{RF} = \omega_{LB} = \omega_{RB}

轮系结构图如下：

逆运动学​

对四舵轮机器人轮系而言，逆解已知量为[vxvyωz]\left[\begin{array}{l} v_{x} \\ v_{y} \\ \omega_{z} \end{array}\right]，逆解待解量为[VLFVRFVLBVRBALFARFALBARB]\left[\begin{array}{l} V_{LF} \\ V_{RF} \\ V_{LB} \\ V_{RB} \\ A_{LF} \\ A_{RF} \\ A_{LB} \\ A_{RB} \end{array}\right]。

上式中每个变量的含义：

  • vxv_x ： 机器人局部坐标系x方向线速度
  • vyv_y ： 机器人局部坐标系y方向线速度
  • ωz\omega_z ： 机器人局部坐标系绕z轴旋转角速度
  • VLFV_{LF} ： 左前舵轮驱动轮线速度（m/s）
  • VRFV_{RF} ： 右前舵轮驱动轮线速度（m/s）
  • VLBV_{LB} ： 左后舵轮驱动轮线速度（m/s）
  • VRBV_{RB} ： 右后舵轮驱动轮线速度（m/s）
  • ALFA_{LF} ： 左前舵轮转向轮角度（Rad）
  • ARFA_{RF} ： 右前舵轮转向轮角度（Rad）
  • ALBA_{LB} ： 左后舵轮转向轮角度（Rad）
  • ARBA_{RB} ： 右后舵轮转向轮角度（Rad）

由三角形关系可得：

RLF2=[L+Rsin⁡(A)]2+[L+Rcos⁡(A)]2(1)R_{LF}^{2}=\left[ L + R\sin(A) \right]^{2}+\left[ L + R\cos(A) \right]^{2} \tag{1}
RLB2=[L−Rsin⁡(A)]2+[L+Rcos⁡(A)]2(2)R_{LB}^{2}=\left[ L - R\sin(A) \right]^{2}+\left[ L + R\cos(A) \right]^{2} \tag{2}
RRF2=[−L+Rcos⁡(A)]2+[L−Rsin⁡(A)]2(3)R_{RF}^{2}=\left[ -L + R\cos(A) \right]^{2}+\left[ L - R\sin(A) \right]^{2} \tag{3}
RRB2=[−L+Rcos⁡(A)]2+[L+Rsin⁡(A)]2(4)R_{RB}^{2}=\left[ -L + R\cos(A) \right]^{2}+\left[ L + R\sin(A) \right]^{2} \tag{4}
tan⁡(π2−ALF)=Rcos⁡(A)+L2Rsin⁡(A)+L2(5)\tan \left(\frac{\pi}{2}-A_{LF}\right)=\frac{ R \cos(A) + \frac{L}{2} }{ R \sin(A) + \frac{L}{2} } \tag{5}
tan⁡(π2−ALB)=Rcos⁡(A)+L2−Rsin⁡(A)+L2(6)\tan \left(\frac{\pi}{2}-A_{LB}\right)=\frac{ R \cos(A) + \frac{L}{2} }{ -R \sin(A) + \frac{L}{2} } \tag{6}
tan⁡(π2−ARF)=Rcos⁡(A)−L2Rsin⁡(A)+L2(7)\tan \left(\frac{\pi}{2}-A_{RF}\right)=\frac{ R \cos(A) - \frac{L}{2} }{ R \sin(A) + \frac{L}{2} } \tag{7}
tan⁡(π2−ARB)=Rcos⁡(A)−L2−Rsin⁡(A)+L2(8)\tan \left(\frac{\pi}{2}-A_{RB}\right)=\frac{ R \cos(A) - \frac{L}{2} }{ -R \sin(A) + \frac{L}{2} } \tag{8}

上式中：

  • LL ： 机器人中心到每个轮子之间的距离
  • AA ： 机器人旋转中心与车体两轮连线的中点形成的夹角
  • RR ： 机器人几何中心与旋转中心的距离
  • RlFR_{lF} ： 机器人旋转中心与左前轮连线距离
  • RRFR_{RF} ： 机器人旋转中心与右前轮连线距离
  • RLBR_{LB} ： 机器人旋转中心与左后轮连线距离
  • RRBR_{RB} ： 机器人旋转中心与右后轮连线距离

在该解算中，根据物理关系有：

V=vx+vy(9)V=\sqrt{v_{x}+v_{y}}\tag{9}
A=arctan⁡(vyvx)(10)A=\arctan \left(\frac{v_{y}}{v_{x}}\right)\tag{10}
V=Rωz(11)V=R \omega_z\tag{11}
VLF=RLFωLF(12)V_{LF}=R_{LF} \omega_{LF}\tag{12}
VRF=RRFωRF(13)V_{RF}=R_{RF} \omega_{RF}\tag{13}
VLB=RLBωLB(14)V_{LB}=R_{LB} \omega_{LB}\tag{14}
VRF=RRFωRF(15)V_{RF}=R_{RF} \omega_{RF}\tag{15}

联立式(9)(9)、(11)(11)可得解得 RR：

R=Vωz=vx+vyωz(16)R = \frac{V}{\omega_z} = \frac{\sqrt{v_{x}+v_{y}}}{\omega_z} \tag{16}

联立式(1)(1)、(10)(10)、(16)(16)可解得RLFR_{LF}，带入式(12)(12)可计算出 VLFV_{LF}
联立式(2)(2)、(10)(10)、(16)(16)可解得RRFR_{RF}，带入式(13)(13)可计算出 VRFV_{RF}
联立式(3)(3)、(10)(10)、(16)(16)可解得RLBR_{LB}，带入式(14)(14)可计算出 VLBV_{LB}
联立式(4)(4)、(10)(10)、(16)(16)可解得RRBR_{RB}，带入式(15)(15)可计算出 VRBV_{RB}
联立式(5)(5)、(10)(10)、(16)(16)可计算出 ALFA_{LF}
联立式(6)(6)、(10)(10)、(16)(16)可计算出 ARFA_{RF}
联立式(7)(7)、(10)(10)、(16)(16)可计算出 ALBA_{LB}
联立式(8)(8)、(10)(10)、(16)(16)可计算出 ARBA_{RB}

综上，此时已得到所有逆解待解量，在代码中实现的时候依然要注意arctan⁡\arctan等反三角函数的奇点问题。

正运动学​

未完待续

待续...

三舵轮轮系​

正在添加...

正运动学​

未完待续

待续...

逆运动学​

未完待续

待续...

双舵轮轮系​

介绍演示​

轮系结构​

如图所示，建立如下世界坐标系 XOYXOY ，世界坐标系中 XX 正方向为机器人全局0度方向，建立机器人本地坐标系 xoyxoy ，车头方向为本地坐标系 xx 正方向。

机器人中心到前后轮子的距离都为LL，机器人旋转角速度为ω\omega，逆时针方向为角速度正方向，机器人本体与轮子作为一个刚体，刚体中每个点的旋转角速度相等，因此有:

ω=ωF=ωB\omega = \omega_{F} = \omega_{B}

逆运动学​

对双舵轮机器人轮系而言，逆解已知量为[vxvyωz]\left[\begin{array}{l} v_{x} \\ v_{y} \\ \omega_{z} \end{array}\right]，逆解待解量为[VFAFVBAB]\left[\begin{array}{l} V_{F} \\ A_{F} \\ V_{B} \\ A_{B} \end{array}\right]。

上式中每个变量的含义：

  • vxv_x ： 机器人局部坐标系x方向线速度
  • vyv_y ： 机器人局部坐标系y方向线速度
  • ωz\omega_z ： 机器人局部坐标系绕z轴旋转角速度
  • VFV_F ： 前舵轮驱动轮线速度（m/s）
  • AFA_F ： 前舵轮转向轮角度（Rad）
  • VBV_B ： 后舵轮驱动轮线速度（m/s）
  • ABA_B ： 后舵轮转向轮角度（Rad）

由三角形关系可得：

RF2=[L+Rcos⁡(π2−A)]2+[Rsin⁡(π2−A)]2(1)R_{F}^{2}=\left[L+R \cos \left(\frac{\pi}{2}-A\right)\right]^{2}+\left[R \sin \left(\frac{\pi}{2}-A\right)\right]^{2} \tag{1}
RB2=[L−Rcos⁡(π2−A)]2+[Rsin⁡(π2−A)]2(2)R_{B}^{2}=\left[L-R \cos \left(\frac{\pi}{2}-A\right)\right]^{2}+\left[R \sin \left(\frac{\pi}{2}-A\right)\right]^{2} \tag{2}
tan⁡(π2−AF)=Rsin⁡(π2−A)L−Rcos⁡(π2−A)(3)\tan \left(\frac{\pi}{2}-A_{F}\right)=\frac{R \sin \left(\frac{\pi}{2}-A\right)}{L-R \cos \left(\frac{\pi}{2}-A\right)} \tag{3}
tan⁡(π2−AB)=Rsin⁡(π2−A)L+Rcos⁡(π2−A)(4)\tan \left(\frac{\pi}{2}-A_{B}\right)=\frac{R \sin \left(\frac{\pi}{2}-A\right)}{L+R \cos \left(\frac{\pi}{2}-A\right)} \tag{4}

上式中：

  • LL ： 机器人中心到每个轮子之间的距离
  • AA ： 机器人旋转中心与车体两轮连线的中点形成的夹角
  • RR ： 机器人几何中心与旋转中心的距离
  • RFR_F ： 机器人旋转中心与前轮连线距离
  • RBR_B ： 机器人旋转中心与后轮连线距离

在该解算中，默认已知关系有：

V=vx+vy(5)V=\sqrt{v_{x}+v_{y}}\tag{5}
A=arctan⁡(vyvx)(6)A=\arctan \left( \frac{v_{y}}{v_{x}} \right) \tag{6}
V=Rωz(7)V=R \omega_z\tag{7}
VF=RFωz(8)V_{F}=R_{F} \omega_z\tag{8}
VB=RBωz(9)V_{B}=R_{B} \omega_z\tag{9}

联立式(5)(5)、(7)(7)可得RR：

R=Vωz=vx+vyωz(10)R = \frac{V}{\omega_z} = \frac{\sqrt{v_{x}+v_{y}}}{\omega_z} \tag{10}

联立式(1)(1)、(6)(6)、(10)(10)可得RFR_F，带入式(8)(8)可计算出 VFV_F
联立式(2)(2)、(6)(6)、(10)(10)可得RBR_B，带入式(9)(9)可计算出 VBV_B
联立式(3)(3)、(6)(6)、(10)(10)可计算出 AFA_F
联立式(4)(4)、(6)(6)、(10)(10)可计算出 ABA_B

综上，此时已得到 VFV_F、VBV_B、AFA_F、ABA_B ，逆解待解量计算完成，在代码中实现的时候依然要注意arctan⁡\arctan等反三角函数的奇点问题。

正运动学​

未完待续

待续...

单舵轮轮系​

介绍演示​

轮系结构​

如下图所示，本文研究的单舵轮 AGV 的结构包括1个主动轮、2个定向轮和1个万向轮，其中主动轮为舵轮，有驱动和转向的功能。万向轮主要起支撑作用，提高AGV承载能力和稳定性，对运动学模型没有影响。定义AGV前面两个从动轮中心连线的中点OO作为 AGV 的参考点，OXYOXY 为小车局部坐标系。

逆运动学​

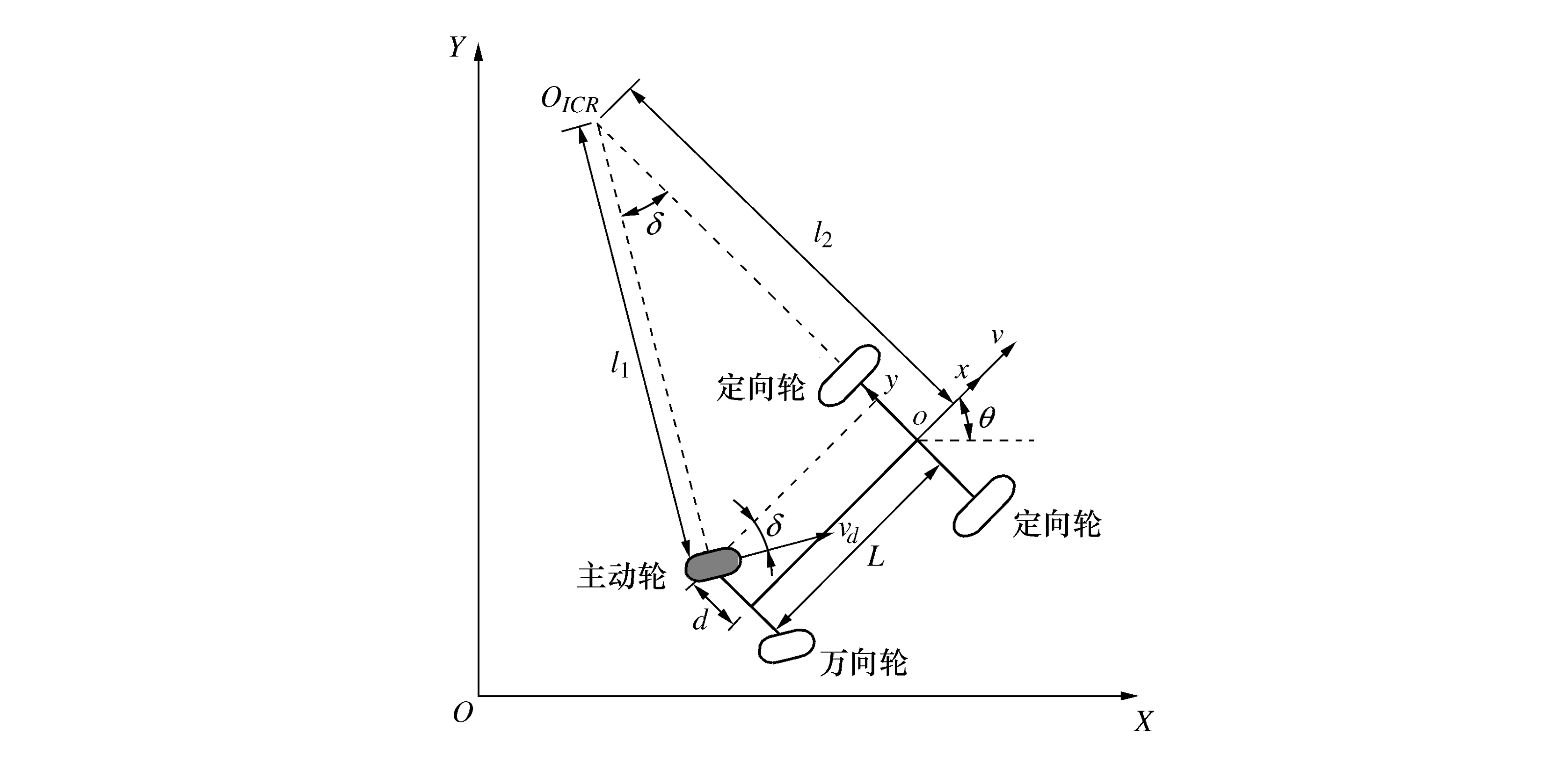
在全局坐标系OXYOXY中，有

[x˙y˙θ˙]=[cos⁡θ0sin⁡θ001]⋅[vω](1)\left[\begin{array}{c} \dot{x} \\ \dot{y} \\ \dot{\theta} \end{array}\right]=\left[\begin{array}{cc} \cos \theta & 0 \\ \sin \theta & 0 \\ 0 & 1 \end{array}\right] \cdot\left[\begin{array}{l} v \\ \omega \end{array}\right] \tag{1}

式中： vv 和 ωω（定义逆时针旋转为正）分别为 AGV 在参考点OO处的线速度和角速度。

根据图中的几何关系可得:

{l1=L/sin⁡δl2=L/tan⁡δ+d(2)\left\{\begin{array}{l} l_{1}=L / \sin \delta \\ l_{2}=L / \tan \delta+d \end{array}\right. \tag{2}

式中 LL 为 AGV 前轮轴心线与后轮轴心线的间距； dd 为舵轮横向偏距；δδ 为舵轮偏转角，定义逆时针为正。 参考点处的线速度 vv 与角速度 ωω 表达式分别为：

{v=ω⋅l2ω=vd/l1(3)\left\{\begin{array}{l} v=\omega \cdot l_{2} \\ \omega=v_{d} / l_{1} \end{array}\right. \tag{3}

式中 vdv_d 为舵轮驱动速度。

将式(2)代入式(3)可得:

{v=vd(cos⁡δ+dsin⁡δL)ω=vdsin⁡δL(4)\left\{\begin{array}{l} v=v_{d}\left(\cos \delta+\frac{d \sin \delta}{L}\right) \\ \omega=\frac{v_{d} \sin \delta}{L} \end{array}\right. \tag{4}

结合式(1)和式(4)可得，单舵轮 AGV 运动学模型为：

{x˙=vdcos⁡θ(cos⁡δ+dsin⁡δL)y˙=vdsin⁡θ(cos⁡δ+dsin⁡δL)θ˙=vdsin⁡δL(5)\left\{\begin{array}{l} \dot{x}=v_{d} \cos \theta\left(\cos \delta+\frac{d \sin \delta}{L}\right) \\ \dot{y}=v_{d} \sin \theta\left(\cos \delta+\frac{d \sin \delta}{L}\right) \\ \dot{\theta}=\frac{v_{d} \sin \delta}{L} \end{array}\right. \tag{5}

正运动学​

未完待续

待续...

Last updated on